Weighted Quick Union & Quick Find Algorithm in Ruby

Today we're going to explore a Ruby implementation of the Weighted Quick Union & Quick Find algorithm. This is an algorithm used to find if there is a connection between two nodes.

Imagine a complicated maze and ask the question of whether you can get from the start of the maze to the end. Is there a path through the maze? Another problem this algorithm can solve is whether 2 computers can communicate with each other. Is there a network connection that goes from Computer A to Computer B?

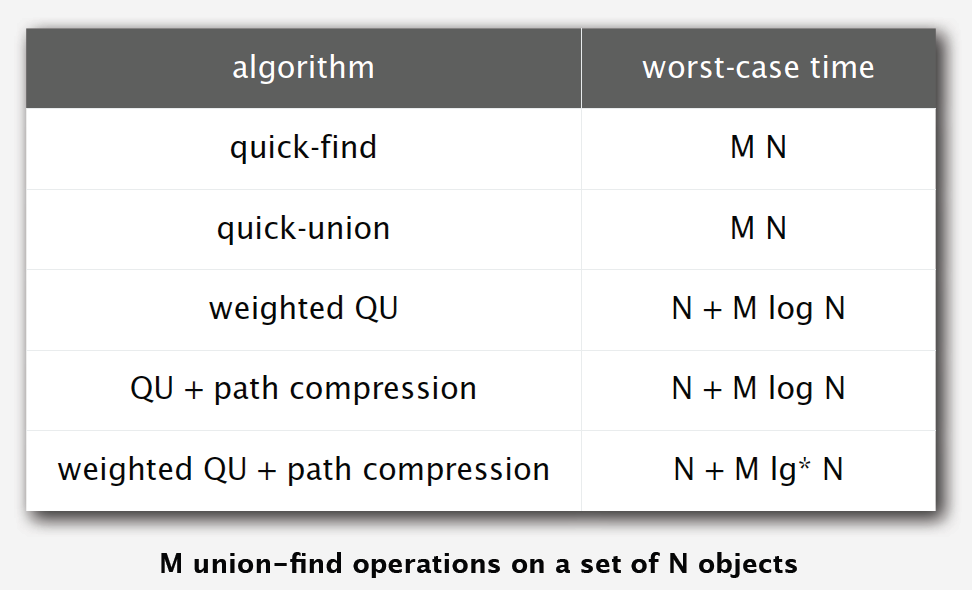
Components

This algorithm is made up of 3 methods. We'll explore each of the methods in detail and then look for ways to make our code faster. First things first: What are we actually trying to accomplish?

What we want to do is to find out whether 2 nodes share a common root node. If the nodes share a common root node we can say that they are connected. In other terms, there is a path from one node to another.

Data Structure

We will store this information in a tree which has its base data type as an Array. Each array element will store a link to its parent. If it is at the top of the tree it will store a reference to itself.

Initialization

To start things off we will need to tell our class how many nodes there are going to be and initialize them to point to themselves.

class UnionFind
  attr_accessor :nodes

  def initialize(num)
    self.nodes = []
    num.times do |n|
      self.nodes[n] = n
    end
  end
end

Root

Next we want to implement a method which will help us find the root of any specific node. We have defined the root as a node which references itself.

def root(i)
  while nodes[i] != i do
    i = nodes[i]
  end
  i
end

Are two nodes connected?

This is actually the simplest method to implement. To find out if two nodes are connected we simply have to find their roots. If they share the same root, they are connected.

def connected?(i, j)
  root(i) == root(j)
end

Union

To join two nodes together we have to make the root of one node equal to the root of the node we are trying to join. If they already share a common root we don't have to do anything... the work had already been done.

def union(i, j)
  rooti = root i
  rootj = root j
  return if rooti == rootj
  nodes[rooti] = rootj
end

Making things faster

We now have a working Quick Union Find class, but let's not stop there. There are 2 pretty easy changes we can make to make our algorithm more performant.

Flatten the trees!

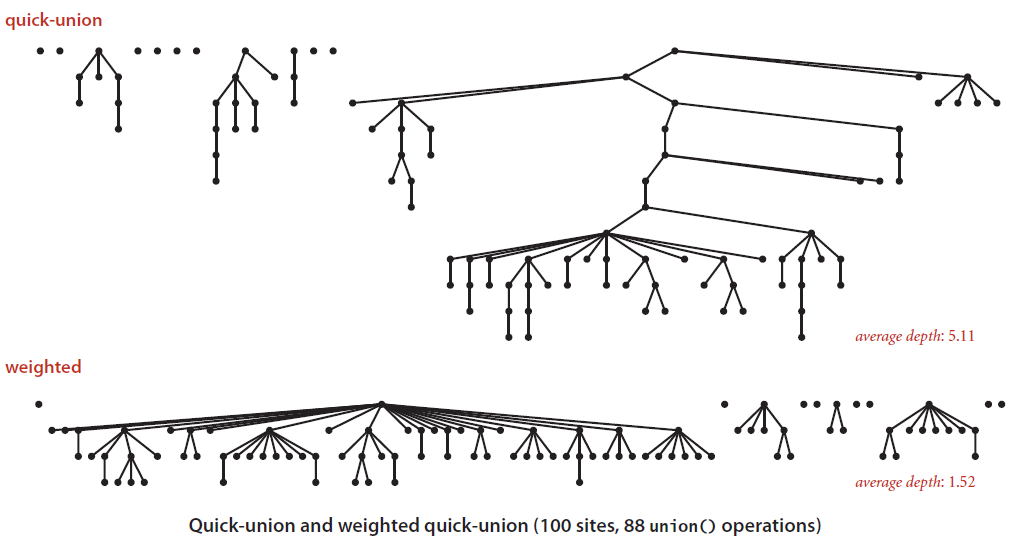
The first thing we can do is to aim for flatter trees. If a tree grows too tall, it takes more work for our root method to traverse the tree to find the root. If we can keep things flatter there will be less steps to get to the top, and therefore will perform more quickly.

To do this we can keep track of the height of each tree, and choose to join the root of the smaller tree to the root of the larger tree. We will need to make 2 changes to our code for this to work:

Update our initialize method to have a sizes array.

class UnionFind
  attr_accessor :nodes, :sizes

  def initialize(num)
    self.nodes = []
    self.sizes = []

    num.times do |n|
      self.nodes[n] = n
      self.sizes[n] = 1
    end
  end
end

And secondly make changes in our union method to decide which root node gets joined to the other.

def union(i, j)
  rooti = root i
  rootj = root j

  # already connected
  return if rooti == rootj

  # root smaller to root of larger
  if sizes[i] < sizes[j]
    nodes[rooti] = rootj
    sizes[rootj] += sizes[rooti]
  else
    nodes[rootj] = rooti
    sizes[rooti] += sizes[rootj]
  end
end

The trees must be flatter!

Lastly, we can get more performance out of our algorithm by compressing the paths as we traverse up them in our root method. What we are essentially doing is cutting the number of steps in half each time. We do this by making our current node have its parent root node.

def root(i)
  # Loop up the chain until reaching root
  while nodes[i] != i do
    # path compression for future lookups
    nodes[i] = nodes[nodes[i]]
    i = nodes[i]
  end
  i
end

Final solution

Here is our final solution of the Weighted Quick Union Find algorithm with Path Compression:

class UnionFind

  attr_accessor :nodes, :sizes

  def initialize(num)
    self.nodes = []
    self.sizes = []

    num.times do |n|
      self.nodes[n] = n
      self.sizes[n] = 1
    end
  end

  def root(i)
    # Loop up the chain until reaching root
    while nodes[i] != i do
      # path compression for future lookups
      nodes[i] = nodes[nodes[i]]
      i = nodes[i]
    end
    i
  end

  def union(i, j)
    rooti = root i
    rootj = root j

    # already connected
    return if rooti == rootj

    # root smaller to root of larger
    if sizes[i] < sizes[j]
      nodes[rooti] = rootj
      sizes[rootj] += sizes[rooti]
    else
      nodes[rootj] = rooti
      sizes[rooti] += sizes[rootj]
    end
  end

  def connected?(i, j)
    root(i) == root(j)
  end

end

Here is an example when using the class:

u = UnionFind.new(10)

p u.nodes
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

p u.connected?(1, 4)
# false

u.union(1,2)
u.union(2,3)
u.union(3,4)

p u.nodes
# [0, 1, 1, 1, 1, 5, 6, 7, 8, 9]

p u.connected?(1,4)
# true